Cara Mencari Luas Setengah Lingkaran, Lengkap Penjelasan, Rumus dan Contoh

Lingkaran salah satu dari sekian jenis bangun datar yang dipelajari dalam pelajaran Matematika. Bangun datar lingkaran contohnya adalah ban mobil, piring, alas cangkir, jam dinding, koin, dan lain-lain. Pada artikel kali ini, kita akan belajar bersama tentang cara mencari luas setengah lingkaran, lengkap dengan penjelasan, rumus dan contohnya.

Mencari luas setengah lingkaran sangat mudah sekali. Untuk mencari luas setengah lingkaran, sebelumnya kamu harus memahami pengertian, unsur, sifat dan rumusnya. Berikut ini kami akan memberikan penjelasan lengkap tentang lingkaran dan cara mencari luas setengah lingkaran.

Pengertian, Unsur, Sifat dan Rumus Setengah Lingkaran

Pengertian Lingkaran
Lingkaran merupakan bangun datar yang tidak memiliki siku-siku. Benda-benda dalam bentuk lingkaran di kehidupan sehari-hari, seperti ban mobil, piring, alas cangkir, jam dinding, koin, dan lain-lain. Lingkaran adalah bangun datar yang tersusun dari kurva dan bukan garis lurus sehingga tidak termasuk poligon.

Ciri-ciri lingkaran yaitu memiliki diameter yang membaginya menjadi dua sisi seimbang dan memiliki jumlah sudut sebesar 180 derajat. Selain itu, diameter konstan dan jari-jari yang menghubungkan titik pusat dengan titik busur lingkaran juga menjadi ciri-ciri dari sebuah lingkaran.

Lingkaran hanya memiliki satu sisi dengan simetri lipat lingkaran yang tak terhingga sebagai salah satu sifatnya. Kemudian sifat lingkaran juga memiliki simetri putar lingkaran yang tak terhingga.

Unsur-Unsur Lingkaran
Berikut unsur-unsur dalam lingkaran:

1. Titik Pusat (P)
Titik pusat merupakan unsur lingkaran pertama yang perlu kamu ketahui. Titik yang berada tepat di bagian tengah lingkaran disebut titik pusat. Jarak titik pusat dengan semua titik pada bangun datar yang satu ini selalu sama.

2. Jari-jari Lingkaran (r)
Unsur selanjutnya ialah jari-jari lingkaran. Jari-jari dapat diartikan sebagai jarak antara titik pusat lingkaran dengan titik pada lingkaran. Panjang jari-jari pada sebuah lingkaran selalu sama karena jarak antara titik pusat dengan semua titik pada lingkaran sama. Dalam rumus matematika, jari-jari kerap disimbolkan dengan huruf r atau yang disebut radius.

3. Diameter (d)
Diameter adalah unsur lingkaran berikutnya yang akan dibahas. Panjang garis lurus yang menghubungkan dua titik pada keliling lingkaran dan melalui titik pusat lingkaran dapat diartikan sebagai diameter. Dapat dikatakan bahwa nilai diameter lingkaran merupakan dua kali nilai jari-jari lingkaran. Diameter kerap disimbolkan dengan huruf d.

4. Busur
Busur adalah bagian lingkaran yang berbentuk garis lengkung merupakan pengertian dari busur. Jenis busur dalam lingkaran terbagi menjadi dua, yakni busur besar dan busur kecil. Busur yang panjangnya lebih dari setengah keliling lingkaran disebut sebagai busur besar. Sementara busur yang panjangnya kurang dari setengah keliling lingkaran disebut busur kecil.

5. Tali Busur
Garis lurus yang menghubungkan dua titik pada lingkaran disebut sebagai tali busur. Garis lurus tersebut mengaitkan dua titik pada keliling lingkaran, tetapi tidak melewati titik pusat lingkaran. Tali busur lingkaran sama seperti tali pada busur panah.

6. Juring
Daerah yang diapit oleh dua jari-jari dan busur lingkaran merupakan pengertian dari juring sebagai unsur lingkaran. Juring pada lingkaran terdiri atas dua bagian, yakni juring besar dan juring kecil. Dimana daerah dalam lingkaran yang dibatasi jari-jari dan busur besar lingkaran disebut juring besar. sementara daerah dalam lingkaran yang dibatasi jari-jari dan busur kecil disebut sebagai juring kecil.

7. Tembereng
Daerah yang diapit oleh tali busur dan busur lingkaran dapat diartikan sebagai tembereng. Kemudian tembereng terbagi menjadi dua, yakni tembereng besar dan tembereng kecil. Daerah yang dibatasi oleh tali busur dan busur besar lingkaran disebut sebagai tembereng besar. Sedangkan daerah yang dibatasi oleh tali busur dan busur kecil lingkaran disebut tembereng kecil.

8. Apotema
Apotema adalah ruas garis tegak lurus yang menghubungkan titik pusat lingkaran dengan tali busur lingkaran diartikan sebagai apotema. Kemudian apotema juga dapat diartikan sebagai jarak terpendek tali busur dengan titik pusat lingkaran.

9. Sudut Pusat
Sudut pusat adalah sebuah sudut yang terbentuk karena pertemuan antara dua tali busur dengan satu titik pada keliling lingkaran disebut sebagai sudut pusat.

10. Sudut Keliling
Sudut keliling adalah sudut yang dibentuk oleh perpotongan antara dua buah tali busur di suatu titik pada keliling lingkaran dapat dikatakan sebagai sudut keliling.

sebaliknya, sesuai dengan bentuknya bisa dari segala arah.

Sifat Lingkaran
Berikut ini adalah sifat-sifat lingkaran:

- Hanya memiliki satu sisi.

- Tidak memiliki sudut.

- Memiliki simetri lipat dan simetri putar yang tak hingga.

- Jarak antara titik pusat dengan sisi manapun selalu sama.

Rumus Lingkaran

Rumus Luas dan Keliling Lingkaran
Lingkaran memiliki bentuk lengkung atau melingkar pada seluruh sisinya. Sebelum masuk ke setengah lingkaran, ada baiknya tahu rumus luas dan keliling lingkaran karena itu adalah asal mula dari rumus setengah lingkaran.

Rumus Keliling lingkaran adalah:

K = 2πr (Jika diketahui jari-jari)

K = πd (Jika diketahui diameter)

Rumus luas lingkaran adalah:

L = π × r × r atau L = πr²

Keterangan:
L = merupakan lambang luas lingkaran.
K = keliling lingkaran
r = jari-jari
d= diameter
π = 22/7 atau 3,14.

Rumus Luas dan Keliling Setengah Lingkaran
Untuk rumus keliling dan luasnya dapat ditemukan dengan mengalikanya dengan ½.

Rumus mencari luas setengah lingkaran:

Luas = π r² ½

Rumus mencari keliling setengah lingkaran:

Keliling = π D ½ atau Keliling = π r

Contoh 

1. Carilah Luas dan Keliling Setengah Lingkaran tersebut: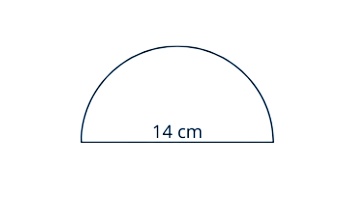

Untuk memudahkan perhitungan, kita bisa langsung menggunakan nilai pi sebesar 22/7. Karena yang diketahui adalah diameter, untuk mengerjakan rumus luas, jangan lupa dibagi 2 dahulu untuk mengetahui jari-jarinya.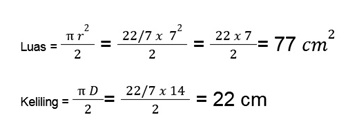

2. Berapakah keliling setengah lingkaran jika diketahui diameternya adalah 20 cm?
Jawaban:
d = 2 x r
r = d : 2
r = 20 : 2
r = 10 cm

Keliling 1/2 lingkaran (K) = (π x r) + d
K = (3,14 x 10) + 20

K = 31,4 + 20

K = 51,4 cm

(m. taufik naufal/nf)